报告题目：q-Coxeter matrix and q-Cartan matrix for a homogeneous bound quiver

报 告 人：杨士林教授（北京工业大学）

报告时间：2023年10月21日 8:00-8:40

报告地点：数学楼301

报告摘要：In this talk, we introduce the concept of q-Coxeter transformation and q-Coxeter matrix for a connected acyclic bound quiver (Q, I) with a homogeneous relations I, then we establish the relationship between q-Coxeter matrix and q-Cartan matrix of (Q, I).

报告人简介：杨士林，北京工业大学理学部教授、博士生导师。分别于1999年4月-2000年4月、 2005年2月-2006年2月在德国Bielefeld大学数学系、斯图加特大学数学系学习和访问.美国《数学评论》、德国《数学评论》评论员。主要研究领域：代数表示论，量子群及Hopf代数的结构、表示等。已在《Letter Math. Phys》、《Journal of Algebra》,《J. Math. Phys》等国际数学期刊上发表90余篇论文。先后承担多项国家自然科学基金、省部级基金等。

报告题目：Leonard对的基本理论

报 告 人：刘军丽教授（廊坊师范学院）

报告时间：2023年10月21日 8:40-9:20

报告地点：数学楼301

报告摘要：Leonard pairs were introduced by Terwilliger to extend the algebraic approach of Bannai and Ito to a result of D. Leonard concerning the sequences of orthogonal polynomials with discrete support for which there is a dual sequence of

orthogonal polynomials. Because these polynomials frequently arise in connection with the finite-dimensional representations of good Lie algebras and quantum groups, it is natural to find Leonard pairs associated with these algebraic objects.

This report presents the concept of Leonard pairs and some concrete examples. Using these examples we illustrate how Leonard pairs arise in the theory of orthogonal polynomials, combinatorics, and representation theory of Lie algebra and quantum group.

报告人简介：刘军丽，廊坊师范学院教授。河北省“三三三人才工程”第三层次人选. 刘军丽博士于河北农业大学获学士学位，于北京工业大学获硕士学位和博士学位。主要从事(弱)Hopf代数、量子群及其表示论、代数组合等方面的相关研究，发表论文20篇。

报告题目：中心荷小于1的有理顶点算子代数的分类

报 告 人：艾春瑞副教授（郑州大学）

报告时间：2023年10月21日 9:20-10:00

报告地点：数学楼301

报告摘要：In this talk, we discuss the classification of rational vertex operator algebras of small central charge. We first discuss the classification of preunitary vertex operator algebras of central charge less than 1. We next discuss the classification of nonunitary rational vertex operator algebras of effective central charge less than 1. The key idea in the classification is to use modular invariant.

The talk is from joint works with Chongying Dong and Xingjun Lin.

报告人简介：艾春瑞，郑州大学副教授。艾春瑞博士于北京工业大学获硕士学位，于四川大学获博士学位。主要研究方向为李代数及顶点算子代数。在Trans. AMS，J.Algebra等杂志上发表多篇论文。

报告题目：Frobenius-Perron theory

报 告 人：王艳华教授 (上海财经大学)

报告时间：2023年10月21日 10:20-11:00

报告地点：数学楼301

报告摘要：The Frobenius–Perron theory of an endofunctor of a category was introduced in recent years. I will introduce the Frobenius-Perron dimension of an endofunctor and provide some applications.

报告人简介：王艳华，上海财经大学数学学院教授、博士生导师，上海市杨浦区妇联兼职副主席，中国教育数学常务理事，上海市工业与应用数学学会常务理事，上海市妇女代表，上海市杨浦区政协委员。主要从事Hopf代数与非交换代数不变量的相关研究，主持多项国家自然科学基金和上海市基金项目，在Adv. Math., Math. Z.，J. Algebra等杂志发表论文约30篇。

报告题目：Canonical comultiplication and double centraliser property

报 告 人：高楠教授（上海大学）

报告时间：2023年10月21日 11:00-11:40

报告地点：数学楼301

报告摘要：In this talk, we show the existence of the attached comultiplication structure on gendo-Gorenstein algebras. Then we give a sufficient and necessary condition for a gendo-Gorenstein algebra to be Gorenstein, and a bocs-theoretic characterisation of the double centraliser property.

The talk is from joint works with Jing Ma and Juxia Zhang.

报告人简介：高楠，上海大学理学院数学系教授、博士生导师，上海市“东方学者”特聘教授。 主要研究领域：代数表示论，三角范畴，导出范畴，Gorenstein同调代数。已在《Comm.Contem.Math.》、《Journal of Algebra》等知名数学期刊上发表30多篇论文。多次受邀在国内外重要学术会议上做报告：世界华人数学家大会45分钟邀请报告。主持多项国家自然科学基金。

报告题目： Rigid subcategories and related subcategories in  

extriangulated categories

报 告 人：张珍教授（齐鲁师范学院）

报告时间：2023年10月21日 14:00-14:40

报告地点：数学楼301

报告摘要：The notion of extriangulated categories was introduced by Nakaoka and Palu as a simultaneous generalization of exact categories and triangulated categories. Exact categories and extension closed subcategories of a triangulated category are extriangulated categories, while there exist some other examples of extriangulated categories which are neither exact nor triangulated. Hence many results hold on exact categories and triangulated categories can be unified in the same framework

In this talk，we firstly obtained the analogue of a Bongartz completion for functorially finite rigid subcategories in an extriangulated category and then we investigated the properties of n-cluster tilting subcategories in an extriangulated category for any positive integer n and showed some equivalent characterization of them. Particularly, when the extriangulated category is 2-Calabi-Yau, we showed any n-cluster tilting subcategories were in fact cluster tilting for any integer n ≥ 2 and they coincided with strongly contravariantly finite maximal n-rigid subcategories.

报告人简介：张珍，齐鲁师范学院教授，美国《数学评论》杂志评论员。以第一作者发表SCI论文10余篇；主持国家自然科学基金项目1项，山东省自然科学基金1项。主要研究方向为代数学。

报告题目：Twisted relative Rota-Baxter operators on Leibniz algebras and NS-Leibniz algebras

报 告 人：郭双建教授（贵州财经大学）

报告时间：2023年10月21日 14:40-15:20

报告地点：数学楼301

报告摘要：In this talk，we show that a twisted relative Rota-Baxter operator K induces a new Leibniz algebra structure and there is a suitable representation of it. The corresponding Loday-Pirashvili cohomology is called the cohomology of the twisted relative Rota-Baxter operator. As an application of the cohomology, we study deformations of a twisted relative Rota-Baxter operator K. We show that the infinitesimal in a formal deformation of K is a 1-cocycle in the cohomology of K.

Moreover, we define a notion of equivalence between two formal deformations of $K$. The infinitesimals corresponding to equivalent deformations are shown to be cohomologous. We introduce Nijenhuis elements associated with a twisted relative Rota-Baxter operator that are obtained from trivial linear deformations. We also find a sufficient condition for the rigidity of a twisted relative Rota-Baxter operator in terms of Nijenhuis elements.

In the last, we introduce a new algebraic structure, called NS-Leibniz algebras. We show that Ns-Leibniz algebras split Leibniz algebras and the underlying structure of a twisted relative Rota-Baxter operator. NS-Leibniz algebras also arise from Nijenhuis operators on Leibniz algebras. Further study on NS-Leibniz algebras is postponed to a forthcoming article.

The talk is from joint work with A. Das.

报告人简介：郭双建，贵州财经大学教授，硕士/博士生导师，美国《数学评论》和德国《数学文摘》杂志评论员。发表SCI论文40余篇；主持省部级及以上课题10项，其中国家自然科学基金项目3项，省级教改项目2项；学术专著2部；中组部“西部之光”访问学者，入选贵州省高等学校优秀科技创新人才支持项目；获贵州省自然科学奖三等奖(排名第1)，第十届贵州省高等教育教学成果奖一等奖(排名第3)，贵州省科学技术进步奖三等奖(排名第4)；贵州财经大学科研先进个人三等奖、青年教师教学技能大赛二等奖、“四有”好老师、优秀工会积极分子、“优秀共产党员”等荣誉称号。目前为贵州省省级基础教育质量监测评估专家，贵州省科技厅专家库专家，河北省科技奖励评审专家，广西壮族自治区科技厅专家库专家。主要研究方向为代数学。

报告题目：The Auslander-Reiten theory in the categories of comodule complexes

报 告 人：付雪荣副教授（菏泽学院）

报告时间：2023年10月21日 15:20-16:00

报告地点：数学楼301

报告摘要：In this talk, we firstly present the Auslander-Reiten sequences of complexes of quasi-finitely comodules over right semiperfect coalgebras. Then we give the structure of Auslander-Reiten triangles for its derived comodule categroies. Furthermore, by defining the Auslander class relative to the cohom functor and the Bass class relative to the cotensor product functor of quasi-finitely comodule categroies, we show that the Auslander-Reiten triangles in derived comodule categroies is closed for the Auslander class and the Bass class, respectively. Finally, we illustrate the above results by concrete examples.

报告人简介：付雪荣，菏泽学院数学与统计学院副教授，主要研究方向：代数表示论与同调代数，主要讲授课程：《近世代数》、《线性代数》、《高等数学》，获山东省微课程教学比赛二等奖一项，获校级优秀教师和“课程思政”优秀教师。 在国内外重要学术刊物上发表论文12篇，其中SCI论文收录7篇。主持山东省自然科学基金一项。

报告题目：A new type restricted quantum group

报 告 人：陈佳蕾副教授（北京工业大学）

报告时间：2023年10月21日 16:20-17:00

报告地点：数学楼301

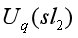报告摘要：In this talk, we define a new type of restricted quantum group and determine its Hopf PBW-deformations in which the classical restricted Drinfeld–Jimbo quantum group is included. We show that is a basic Hopf algebra, then uniformly realize and 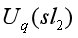via some quotients of (deformed) preprojective algebras corresponding to the Gabriel quiver of .

This is a joint work with Yongjun Xu.

报告人简介：陈佳蕾，北京工业大学理学部副教授，硕士生导师。主要研究领域：Hopf代数、量子群理论。在《J. Math. Phys》等期刊上发表论文十余篇。主持国家自然科学基金青年基金一项，北京市教委科技计划项目一项。

报告题目：The representation ring of a quotient of a prime Hopf algebra of GK-dimension one and their related topics

报 告 人：杨瑞芳博士（山西师范大学）

报告时间：2023年10月21日 17:00-17:40

报告地点：数学楼301

报告摘要：In this talk, we construct all the indecomposable modules of a class of non-pointed Hopf algebra D(n), which are quotient Hopf algebras of a class of prime Hopf algebras of GK-dimension one. Then we establish the decomposition formulas of the tensor product of any two indecomposable modules. Moreover, the representation ring of the Hopf algebra is characterized by generators and some relations. In the last, we investigate the structure of Yetter-Drinfeld simple modules over D(n) and give iso-classes of them.

The talk is from joint works with Professor Shilin Yang.

报告人简介：杨瑞芳，山西师范大学数学与计算机科学学院讲师。2015-2021年在北京工业大学理学部求学（硕博连读），师从杨士林教授，2021年获理学博士学位。主要研究领域为Hopf代数和量子群及其表示，已在《Communications in Algebra》、《Journal of Algebra and Its Applications》等杂志发表SCI论文3篇，主持山西省青年基金一项。